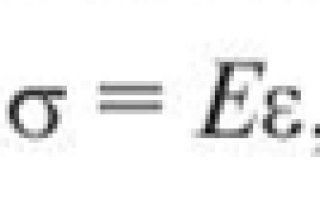Модуль деформации стали

Модуль общей деформации грунта (понятие и особенности)

Модуль общей деформации грунта — представляет собой обобщенную характеристику грунта, отражающую как упругие, так и пластические деформации. [Механика грунтов. Бартоломей А.А.]

Величина модуля общей деформации меняется в процессе воздействия на грунт:

где E_ot — модуль общей деформации грунта в период действия нагрузки t

P — нагрузка;

h — мощность деформируемого слоя;

S_t — полная деформация, успевающая развиться за период времени t.

Модуль общей деформации по сравнению с модулем нормальной упругости имеет следующие отличия [Механика грунтов. Бартоломей А.А.]:

1. В связи с нелинейностью деформаций данное значение модуля общей деформации оказывается справедливым лишь при малых интервалах изменения нагрузки.
2. Модуль общей деформации характеризует зависимость между давлением и деформациями только по ветви загружения; для ветви разгрузки он неприменим.
3. Модуль деформации — величина переменная, изменяющаяся в зависимости от времени действия нагрузки, степени уплотнения грунта, площади и формы штампа, глубины расположения штампа относительно поверхности грунта.
4. Величина модуля упругости грунтов, характеризующая зависимость между давлением и только упругой составляющей деформаций, всегда будет больше, чем модуль общей деформации того же грунта.

Модуль деформации грунта определяют по следующим нормативным документам

• ГОСТ 12248-2010 Грунты. Методы лабораторного определения характеристик прочности и деформируемости.
• ГОСТ 20276-2012 Грунты. Методы полевого определения характеристик прочности и деформируемости

Рассмотрим немного подробнее нормирование методов определения модуля деформации.

Определение лабораторного модуля деформации согласно ГОСТ 12248-2010:

1. Методом одноосного сжатия в соответствии с разделом 5.2. для определения модуля деформации и упругости для полускальных и глинистых грунтов с I_L ≤ 0,25.

Модуль деформации вычисляется по п.5.2.5.3:

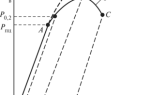
Модуль деформации E в заданном диапазоне напряжений Δσ вычисляют по нагрузочной ветви зависимости ε₁ = f(σ) по формуле:

2. Методом трехосного сжатия в соответствии с разделом 5.3. для определения

модуля деформации любых дисперсных грунтов..

Модуль деформации вычисляется по п.5.2.5.3:

Модуль деформации E определяют при испытаниях, проведенных при постоянном значении напряжений σ₃ ( Δσ₃ =0) и вычисляют по формуле:

Δσ₁ — приращение напряжений σ₁ в заданном диапазоне;

Δε₁ — приращение относительных вертикальной деформации образца.

3. Методом компрессионного сжатия в соответствии с разделом 5.4. для песков мелких и пылеватых, глинистых грунтов, органо-минеральных и органических грунтов.

Модуль деформации вычисляется по п.5.4.6.4:

Модуль деформации E в заданном диапазоне напряжений Δσ вычисляют по нагрузочной ветви зависимости ε₁ = f(σ) по формуле:

5.4.6.4 Одометрический модуль деформации E_oed и модуль деформации по данным компрессионных испытаний E_k , МПа, в заданном интервале давлений Δp (секущие модули) вычисляют с точностью 0,1 МПа по формулам:

E_oed = Δp / Δε (5.33)

где Δε — изменение относительного сжатия, соответствующее Δp;

m_o — коэффициент сжимаемости, соответствующий Δp;

β — коэффициент, учитывающий отсутствие поперечного расширения грунта в компрессионном приборе и вычисляемый по формуле:

β = 1- (2 · υ 2 ) / (1 — υ ) (5.36)

где υ — коэффициент поперечной деформации, определяемый по результатам испытаний в приборах трехосного сжатия по 5.3 или в компрессионных приборах с измерением бокового давления.

При отсутствии экспериментальных данных допускается принимать β равным:

• 0,8 — для песков;
• 0,7 — для супесей;
• 0,6 — для суглинков;
• 0,4 — для глин.

Определение полевого модуля деформации согласно ГОСТ 20276-2012:

1. Методом испытания штампом в соответствии с разделом 5 для определения модуля деформации дисперсных грунтов: минеральных, органо-минеральных и органических грунтов.

Определяют по результатам нагружения грунта вертикальной нагрузкой в забое горной выработки с помощью штампа.

Модуль деформации E вычисляется по п.5.5.2:

K_p — коэффициент, принимаемый в зависимости от заглубления штампа h/D ( h — глубина расположения штампа относительно дневной поверхности грунта, см; D — диаметр штампа, см);

K₁ — коэффициент, принимаемый для жесткого круглого штампа равным 0,79;

Δp — приращение давления на штамп;

ΔS — приращение осадки штампа, соответствующее Δp.

2. Методом испытания радиальным прессиометром в соответствии с разделом 5 для определения модуля деформации дисперсных грунтов: песков, глинистых, органо-минеральных и органических грунтов..

В состав установки для испытания грунта радиальным прессиометром должны входить:

• зонд, снабженный эластичной оболочкой с каналами для передачи давления рабочей жидкости (воздуха) под оболочку;
• устройство для создания и измерения давления в камере зонда;
• устройство для измерения перемещений оболочки зонда.

Модуль деформации E вычисляется по п.5.5.2:

где K_r — корректирующий коэффициент;

r_o — начальный радиус скважины;

Δp — приращение давления на стенку скважины;

ΔS — приращение перемещения стенки скважины (по радиусу).

8.1.2. Упругая деформация. Модули упругости

Упругая деформация возникает в результате смещения атомов из равновесных положений в кристаллической решетке на расстояния, как правило, меньшие периода решетки (см. рис. 8.6, б), и исчезает после прекращения действия внешних сил.

В упругодеформируемом теле после снятия нагрузки происходят обратимые изменения формы и размеров образца, т. е. тело восстанавливает свою исходную форму и первоначальные размеры. Поведение твердых тел при упругой деформации (линейный участок на диаграмме а—г, см. рис. 8.3) описывается законом Гука, который определяет прямую пропорциональность между механическим напряжением и упругой деформацией материала.

Для деформации растяжения закон Гука имеет вид

где Е — модуль нормальной упругости, или модуль Юнга.

Рис. 8.7. Схема деформации сдвига твердого тела

Для сдвиговой деформации при действии касательных напряжений (рис. 8.7) закон Гука также имеет простой вид

где т = F/S — касательное напряжение (F— действующая сила; S — площадь сдвига); G — модуль сдвига; у — относительный сдвиг (ввиду малости угла сдвига у при упругой деформации можно считать у =

Модуль нормальной упругости и модуль сдвига связаны между собой соотношением

где ц — коэффициент Пуассона (отношение относительной поперечной деформации к относительной продольной деформации при растяжении образца в области действия закона Гука). Для большинства металлов р = 0,33-0,4.

При всестороннем сжатии закон Гука выражает прямую пропорциональность между гидростатическим давлением Р и относительным уменьшением объема х = А К/ V:

где К — модуль объемной упругости.

Таким образом, модуль упругости — это величина, равная отношению напряжения к вызванной им упругой относительной деформации.

Рассмотренные модули упругости являются важнейшими характеристиками упругих свойств материала. Они определяют прочность межатомных связей. В таблице 8.1 даны значения упругих постоянных для ряда поликристаллических металлов.

Упругие постоянные поликристаллических металлов при комнатной температуре (А. И. Чижик)

Модули упругости зависят от ряда факторов — температуры, наклепа, легирования материалов.

При нагреве модули упругости несколько уменьшаются (на 2-4% при повышении температуры на 100 °С), поскольку из-за термического расширения увеличиваются межатомные расстояния в материале. Эта зависимость обычно монотонная (рис. 8.8), но монотонность хода кривой может нарушиться в случае каких-либо структурных превращений в материале (полиморфных, фазовых и др.). В частности, на рис. 8.8 виден скачок значения модуля нормальной упругости за счет а—у-превращения в железе при 910‘С.

Следует отметить, что существуют сплавы на железоникелевой основе (Fe + 36% Ni + (7—9)% Cr + (2—3)% Мп), так называемые элинвары, характеризующиеся близким к нулю температурным коэффициентом модуля упругости. Например, в температурном диапазоне от —50 до +60 °С модуль упругости для них постоянен. Такое необычное поведение элинваров при изменении температуры связано с компенсирующим влиянием магнитных эффектов.

Рис. 8.8. Температурные зависимости модуля нормальной упругости для некоторых металлов (Л. С. Мороз)

В связи с такой уникальной особенностью данные сплавы применяют для изготовления камертонов, мембран, часовых пружин и других деталей, которые должны сохранять упругие свойства в заданном температурном интервале.

Нагартовка (наклеп) при небольших степенях пластической деформации слабо влияет на модули упругости (их уменьшение составляет не более 1%). Вообще говоря, для поликристаллов, состоящих из большого числа различно ориентированных зерен, определяемые среднестатистические изменения упругих модулей примерно постоянны и не зависят от направления.

Однако значительная пластическая деформация приводит к образованию в структуре поликристаллических металлов и сплавов преимущественной ориентировки зерен — текстуры деформации, вследствие чего возникает анизотропия механических свойств материала, и значения модулей упругости в различных кристаллографических направлениях могут существенно изменяться (эти изменения иногда достигают десятков процентов). Аналогичным образом на величину упругих модулей может влиять рекристаллизация при нагреве после деформации (при этом образуется текстура рекристаллизации).

Вследствие значительной анизотропии свойств при большой скорости нагружения упругая деформация металла (сплава) может завершиться хрупким разрушением практически без пластической деформации. Модули упругости монокристаллов также являются анизотропными и зависят от межатомного расстояния в соответствующих кристаллографических направлениях кристаллической решетки. Например, для железа в направлении [100] модуль нормальной упругости равен 132 ГПа, а в направлении [1111-271 ГПа.

Легирование материалов может как увеличивать, так и уменьшать модуль упругости. Если силы связи между атомами растворенного элемента и атомами растворителя (основного элемента) больше, чем силы межатомного взаимодействия между атомами растворителя, то при легировании в твердом растворе модуль упругости повышается (и наоборот). При этом модуль упругости изменяется в зависимости от содержания легирующего элемента по закону, близкому к линейному (рис. 8.9).

Если содержание легирующего элемента в кристаллической решетке растворителя превосходит значение предела растворимости при данной температуре, то, как известно, образуется вторая фаза, имеющая свою кристаллическую решетку и собственный модуль упругости. Тогда, подобно рассмотренному выше случаю образования однофазного твердого раствора, модуль упругости может как увеличиться, так и уменьшиться. Если значение модуля упругости у второй фазы больше, чем у основы, то модуль упругости гетерофазного сплава увеличивается с повышением содержания легирующих элементов, образующих вторую фазу (и наоборот). Рисунок 8.10 иллюстрирует влияние некоторых легирующих элементов, образующих твердую вторую фазу в алюминиевых сплавах, на модуль нормальной упругости алюминия.

Рис. 8.9. Влияние легирования на модуль нормальной упругости меди и алюминия (экспериментальные данные:

• —Г. Брэдфилд и др.,
• —-В. Кестер,
• ——Б. Эллиот и др.)

Рис. 8.10. Влияние элементов, образующих вторую фазу, на модуль нормальной упругости алюминия (Н. Дудзински)

Модуль упругости (Модуль Юнга)

Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.

Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.

Общее понятие

При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.

Определение модуля Юнга твердых тел

Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.

Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м 2 или по международной системе Па.

Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σ_z) и лежащая в плоскости сечения – касательное напряжение (τ_z).

Опыт с пружинными весами

Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:

где ε – относительное удлинение или деформация.

Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм 2 или Н/м 2 :

Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.

В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.

Способы расчета модуля упругости

Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.

Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.

Обозначается как Е и выражается в Па или ГПа.

Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):

Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.

Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.

• Через касательные напряжения (τ_z) и угол сдвига (γ):

• Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):

Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:

где F_р – разрушающая сила, Н;

L – расстояние между опорами, мм;

b, h – ширина и толщина образца, мм;

ƒ₁, ƒ₂– прогибы, образованные в результате нагрузки F₁ и F₂.

При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания

Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:

σ = 2με + λtrace(ε)I (7)

Оба параметра могут быть выражены из следующих соотношений:

Модуль упругости различных материалов

Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:

• природы веществ, формирующих состав материала;
• моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
• структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
• плотности материала (распределения частиц в его объеме);
• обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).

Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.

Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:

• бронза – 10,4 ГПа;
• алюминиевая бронза при литье – 10,3 ГПа;
• фосфористая бронза катанная – 11,3 ГПа.

Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.

Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:

• литая – 82 ГПа;
• прокатанная – 108 ГПа;
• деформированная – 112 ГПа;
• холоднотянутая – 127 ГПа.

Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.

Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.

Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.

Модули упругости некоторых материалов

На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:

Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.

Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.

Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.

Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

1. по справочным данным из таблиц;
2. экспериментальными методами для небольшого образца;
3. расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Показатель предела нагрузки на сталь — модуль упругости Юнга

До того, как взять в работу какой-то строительный материал, необходимо изучить его прочностные данные и возможное взаимодействие с другими веществами и материалами, их сочетаемость в плане адекватного поведения при одинаковых нагрузках на конструкцию. Определяющая роль для решения этой задачи отводится модулю упругости – его называют ещё модулем Юнга.

Высокая прочность стали позволяет использовать её при строительстве высотных зданий и ажурных конструкций стадионов и мостов. Добавки в сталь некоторых веществ, влияющих на её качество, называют легированием, и эти добавки могут увеличить прочность стали в два раза. Модуль упругости стали легированной гораздо выше, чем обычной. Прочность в строительстве, как правило, достигается подбором площади сечения профиля в силу экономических причин: высоколегированные стали имеют более высокую стоимость.

Далее, будет рассмотрено значение термина, изменчивость его для стали различных сортов. Для сравнения будут приведены значения модуля других материалов.

Физический смысл

Обозначение модуля упругости как физической величины – (Е), этот показатель характеризует упругую сопротивляемость материала изделия прилагаемым к нему деформирующим нагрузкам:

• продольным – растягивающим и сжимающим;
• поперечным – изгибающим или исполненным в виде сдвига;
• объёмным – скручивающим.

Чем выше значение (Е), тем выше сопротивляемость материала нагрузкам, тем прочнее будет изделие из этого материала и тем выше будет предел разрушения. Например, для алюминия эта величина составляет 70 ГПа, для чугуна – 120, железа – 190, а для стали до 220 ГПа.

Определение

Модуль упругости – сводный термин, вобравший в себя другие физические показатели свойства упругости твёрдых материалов – под воздействием силы изменяться и обретать прежнюю форму после её прекращения, то есть, упруго деформироваться. Это отношение напряжения в изделии – давление силы на единицу площади, к упругой деформации (безразмерная величина, определяемая отношением размера изделия к его изначальному размеру). Отсюда и его размерность, как и у напряжения – отношение силы к единице площади. Поскольку напряжение в метрической СИ принято измерять в Паскалях, то и показатель прочности – тоже.

Существует и другое, не очень корректное определение: модуль упругости – это давление, способное удлинить изделие вдвое. Но предел текучести большого количества материалов значительно ниже прилагаемого давления.

Модули упругости, их виды

Способов изменения условий приложения силы и вызываемых при этом деформаций много, и это предполагает и большое количество видов модулей упругости, но на практике сообразно деформирующим нагрузкам выделяют три основных:

• Юнга (Е) представляет упругую сопротивляемость растягивающим и сжимающим нагрузкам – собственно, именно этим термином пользуются, когда говорят о модуле упругости;
• модуль сдвига (G) характеризует сопротивляемость любому нарушению формы без её разрушения или изменения нормы – это отношение сдвигающей нагрузки к деформации, проявляющейся в виде изменчивости прямого угла между двумя половинами плоскости, подвергшейся нагрузке. Второе название этого термина – жёсткости, он же представляет и вязкость материала;
• модуль объёмной упругости (К) – сопротивляемость изменению объёма при разносторонних нормально приложенных напряжениях, имеющих равную величину по всем векторам. Его называют ещё модулем объёмного сжатия, выражается отношением объёмного давления к объёмной деформации сжатия.

Этими показателями характеристики упругости не исчерпываются, есть и другие, которые несут другую информацию, имеют иную размерность и смысл. Это также широко известные среди специалистов показатели упругости Ламе и коэффициент Пуассона.

Как определить модуль упругости стали

Для определения параметров различных марок стали существуют специальные таблицы в составе нормативных документов в области строительства – в строительных нормах и правилах (СНиП) и государственных стандартах (ГОСТ). Так, модуль упругости (Е) или Юнга, у чугуна белого и серого от 115 до 160 ГПа, ковкого – 155. Что касается стали, то модуль упругости стали С245 – углеродистой имеет значения от 200 до 210 ГПа. Легированная сталь имеет показатели несколько выше – от 210 до 220 ГПа.

Та же самая характеристика у рядовых марок стали Ст.3 и Ст.5 имеет то же значение – 210 ГПа, а у стали Ст.45, 25Г2С и 30ХГС – 200 ГПа. Как видим, изменчивость (Е) для различных марок стали незначительна, а вот в изделиях, например, в канатах – другая картина:

• у прядей и свивок проволоки высокой прочности 200 ГПа;
• стальные тросы с металлическим стержнем 150 ГПа;
• стальные канаты с органическим сердечником 130 ГПа.

Как можно заметить, разница значительная.

Значения модуля сдвига или жёсткости (G) можно увидеть в тех же таблицах, они имеют меньшие значения, для прокатной стали – 84 ГПа, углеродистой и легированной – от 80 до 81 гпа, а для сталей Ст.3 и Ст.45–80 ГПа. Причиной различия значений параметра упругости является одновременное действие сразу трёх основных модулей, рассчитываемых по разным методикам. Однако разница между ними небольшая, что говорит о достаточной точности изучения упругости. Поэтому не стоит зацикливаться на вычислениях и формулах, а следует принять конкретную величину упругости и пользоваться ей как константой. Если не производить вычисления по отдельным модулям, а сделать расчёт комплексно, значение (Е) будет составлять 200 ГПа.

Необходимо понимать, значения эти разнятся для сталей с разными присадками и стальных изделий, включающих детали из других веществ, но разнятся эти значения незначительно. Основное влияние на показатель упругости оказывает содержание углерода, а вот способ обработки стали – горячий прокат или холодная штамповка, значительного влияния не оказывает.

При выборе стальных изделий пользуются также и ещё одним показателем, который регламентируется так же, как и модуль упругости в таблицах изданий ГОСТ и СНиП – это расчётное сопротивление растягивающим, сжимающим и изгибающим нагрузкам. Размерность у этого показателя та же, что и у модуля упругости, но значения на три порядка меньше. Этот показатель имеет два назначения: нормативное и расчётное сопротивление, названия сами говорят за себя – расчётное сопротивление применяется при выполнении расчётов прочности конструкций. Так, расчётное сопротивление стали С255 при толщине проката от 10 до 20 мм – 240 МПа, при нормативном 245 МПа. Расчётное сопротивление проката от 20 до 30 мм чуть ниже и составляет 230 МПа.

Модуль Юнга (упругости) для стали и других материалов — определение, смысл

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Связь с другими модулями упругости

В случае изотропного тела модуль Юнга связан с модулем сдвига и модулем объёмной упругости соотношениями

где — коэффициент Пуассона.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

• Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
• Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
• Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
• Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.

Температурная зависимость модуля Юнга

Температурная зависимость модуля упругости простых кристаллических материалов объясняется исходя из того, что модуль упругости определяется как вторая производная от внутренней энергии по соответствующей деформации . Поэтому при температурах ( — температура Дебая) температурная зависимость модуля упругости определяется простым соотношением

где — адиабатический модуль упругости идеального кристалла при ; — дефект модуля, обусловленный тепловыми фононами; — дефект модуля, обусловленный тепловым движением электронов проводимости

Механические свойства

Только при работе на растяжение или сжатие модуль (Юнга) упругости помогает угадать поведение того или иного материала. А вот при изгибе, срезе, смятии и прочих нагрузках потребуется ввести дополнительные параметры:

1. Жёсткостью называют произведение поперечного сечения профиля на модуль упругости. По этой величине можно судить о пластичности узла конструкции в целом, а не о материале отдельно. Единицей измерения являются килограммы силы.
2. Продольное относительное удлинение — это отношение абсолютного удлинения материала-образца к его общей длине. К примеру, на стержень, длина которого равна 200 миллиметров, приложили некоторую силу. В результате он стал короче на 5 миллиметров. В результате относительное удлинение будет равняться 0,05. Эта величина безразмерная. Для более удобного восприятия иногда её переводят в проценты.
3. Поперечное относительное удлинение рассчитывается точно так же, как и продольное относительное удлинение, но вместо длины берут диаметр стержня. Опытным путём было установлено, что для большего количества материала поперечное меньше продольного удлинения приблизительно в 4 раза.
4. Коэффициент Пуассона. Это отношения относительной продольной к относительной поперечной деформации. При помощи этой величины можно полностью описать под воздействием нагрузки изменения формы.
5. Модуль сдвига описывает упругие свойства под воздействием касательных свойств на образец. Иными словами, когда вектор силы направляется к поверхности тела под 90 градусов. Примером подобных нагрузок служит работа гвоздей на смятие, заклёпок на срез и пр. Этот параметр связан с вязкостью материала.
6. Модуль упругости объёмной характеризует изменение объёма образца для разностороннего равномерного приложения нагрузки. Эта величина является отношением давления объёмного к деформации сжатия объёмной. Как пример можно рассматривать опущенный в воду материал, на который воздействует давление жидкости по всей его площади.

Кроме всего вышесказанного стоит упомянуть, что у некоторых материалов в зависимости от направления нагрузки разные механические свойства. Подобные материалы называются анизотропными. Примерами подобного является ткани, некоторые виды камня, слоистые пластмассы, древесина и прочее.

У материалов изотропных механические свойства и деформация упругая в любом направлении одинаковы. К таким материалам относятся металлы: алюминий, медь, чугун, сталь и прочее, а также каучук, бетон, естественные камни, пластмассы неслоистые.

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

• Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
• Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
• Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
• Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
• Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
• Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
• И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и пос, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.