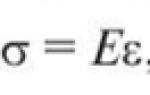Максимально допустимый прогиб металлической балки

Как рассчитать деревянную балку

В частном домостроении есть 3 вида конструкций, которые необходимо подбирать по расчету. Это фундамент, перекрытие и крыша. Конечно, вы можете сделать это и без расчета, опираясь на свой опыт или из опыт своих друзей и знакомых. Но тогда вы рискуете своей безопасностью или своим «кошельком». Другими словами, конструкции могут не выдержать тех нагрузок, которые на них приходятся, или они возводятся с большой надежностью, чем требуется, и на это идут лишние деньги.

Ниже мы рассмотрим, как можно рассчитать деревянную балку, т.е. подобрать ее оптимальное сечение в зависимости от условий эксплуатации и характеристики материала.

Расчет балок должен происходить в следующей последовательности:

1. Сбор нагрузок на балку.

Сбор нагрузок — это та процедура, без которой не обходится ни один расчет. Процедура эта довольно длинная, поэтому она вынесена в отдельную статью, где приведен пример сбора нагрузок на перекрытие и балку.

Для тех же, кому нужно рассчитать балку междуэтажного или чердачного перекрытия и кто не хочет заниматься сбором нагрузок, существует универсальный метод. Он заключается в том, что для междуэтажного перекрытия можно принять расчетную нагрузку равную 400 кг/м2, а для чердачного — 200 кг/м2.

Но иногда эти нагрузки могут быть сильно завышены. Например, когда строится небольшой дачный домик, на втором этаже которого будут располагаться две кровати и шкаф, нагрузку можно взять и 150 кг/м2. Только это исключительно на Ваше усмотрение.

2. Выбор расчетной схемы.

Расчетная схема подбирается в зависимости от способа опирания (жесткая заделка, шарнирное опирание), вида нагрузок (сосредоточенные или распространенные) и количества пролетов.

3. Определение требуемого момента сопротивления.

Это так называемый расчет по первой группе предельных состояний — по несущей способности (прочности и устойчивости). Здесь определяется минимальное допустимое сечение деревянной балки, при котором эксплуатация конструкций будет происходить без риска наступления их полной непригодности к эксплуатации.

Примечание : в расчете используются расчетные нагрузки.

4. Определение максимально допустимого прогиба балки.

Это расчет по второй группе предельных состояний — по деформациям (прогибу и перемещениям). По данному расчету определяется сечение деревянной балки в зависимости о предельного прогиба, при превышении которого будет нарушена нормальная их эксплуатация.

Примечание : в расчет используются нормативные нагрузки.

Теперь конкретнее. Для того, чтобы рассчитать деревянную балку перекрытия, Вы можете воспользоваться специальным калькулятором или примером ниже.

Пример расчета деревянной балки перекрытия.

Расчет выполняется в соответствии со СНиП II-25-80 ( СП 64.13330.2011) «Деревянные конструкции» [1] и применением таблиц [2].

Исходные данные.

Требуется рассчитать балку междуэтажного перекрытия над первым этажом в частном доме.

Материал — дуб 2 сорта.

Срок службы конструкций — от 50 до 100 лет.

Состав балки — цельная порода (не клееная).

Шаг балок — 800 мм;

Длина пролета — 5 м (5 000 мм);

Пропитка антипиренами под давлением — не предусмотрена.

Расчетная нагрузка на перекрытие — 400 кг/м2; на балку — q_р = 400·0,8 = 320 кг/м.

Нормативная нагрузка на перекрытие — 400/1,1 = 364 кг/м2; на балку — q_н = 364·0,8 = 292 кг/м.

Расчет.

1) Подбор расчетной схемы.

Так как балка опирается на две стены, т.е. она шарнирно оперта и нагружена равномерно-распределенной нагрузкой, то расчетная схема будет выглядеть следующим образом:

2) Расчет по прочности.

Определяем максимальный изгибающий момент для данной расчетной схемы:

М_max = q_p·L 2 /8 = 320·5 2 /8 = 1000 кг·м = 100000 кг·см,

где: q_p — расчетная нагрузка на балку;

L — длина пролета.

Определяем требуемый момент сопротивления деревянной балки:

где: R = R_и·m_п·m_д·m_в·m_т·γ_сc = 130·1,3·0,8·1·1·0,9 = 121,68 кг/см 2 — расчетное сопротивление древесины, подбираемое в зависимости от расчетных значений для сосны, ели и лиственницы при влажности 12% согласно СНиП [1] — таблицы 1 [2] и поправочных коэффициентов:

m_п = 1,3 — коэффициент перехода для других пород древесины, в данном случае принятый для дуба (таблица 7 [2]).

m_д = 0,8 — поправочный коэффициент принимаемый в соответствии с п.5.2. [1], вводится в случае, когда постоянные и временный длительные нагрузки превышают 80% суммарного напряжения от всех нагрузок.

m_в = 1 — коэффициент условий работы (таблица 2 [2]).

m_т = 1 — температурный коэффициент, принят 1 при условии, что температура помещения не превышает +35 °С.

γ_сс = 0,9 — коэффициент срока службы древесины, подбирается в зависимости от того, сколько времени вы собираетесь эксплуатировать конструкции (таблица 8 [2]).

γ_н/о = 1,05 — коэффициент класса ответственности. Принимается по таблице 6 [2] с учетом, что класс ответственности здания I.

В случае глубокой пропитки древесины антипиренами к этим коэффициентам добавился бы еще один: m_a = 0.9.

С остальными менее важными коэффициентами вы можете ознакомится в п.5.2 СП 64.13330.2011.

Примечание: перечисленные таблицы вы можете найти здесь.

Определение минимально допустимого сечения балки:

Так как чаще всего деревянные балки перекрытия имеют ширину 5 см, то мы будем находить минимально допустимую высоту балки по следующей формуле:

h = √(6W_треб/b) = √(6·862,92/5) = 32,2 см.

Формула подобрана из условия W_балки = b·h 2 /6. Получившийся результат нас не удовлетворяет, так как перекрытие толщиной более 32 см никуда не годится. Поэтому увеличиваем ширину балки до 10 см.

h = √(6W_треб/b) = √(6·862,92/10) = 22,8 см.

Принятое сечение балки: bxh = 10×25 см.

3) Расчет по прогибу.

Здесь мы находим прогиб балки и сравниваем его с максимально допустимым.

Определяем прогиб принятой балки по формуле соответствующей принятой расчетной схеме:

f = (5·q_н·L 4 )/(384·E·J) = (5·2,92·500 4 )/(384·100000·13020,83) = 1,83 см

где: q_н = 2,92 кг/cм — нормативная нагрузка на балку;

L = 5 м- длина пролета;

Е = 100000 кг/см2 — модуль упругости. Принимается равным в соответствии с п.5.3 СП 64.13330.2011 вдоль волокон 100000 кг/см2 и 4000 кг/см 2 поперек волокон не взирая на породы при расчете по второй группе предельных состояний. Но справедливости ради нужно отметить, что модуль упругости в зависимости от влажности, наличия пропиток и длительности нагрузок только у сосны может колебаться от 60000 до 110000 кг/см2. Поэтому, если вы хотите перестраховаться, то можете взять минимальный модуль упругости.

J = b·h 3 /12 = 10·25 3 /12 = 13020,83 см 4 — момент инерции для доски прямоугольного сечения.

Определяем максимальный прогиб балки:

f_max = L·1/250 = 500/250 = 2,0 см.

Предельный прогиб определяется по таблице 9 [2], как для междуэтажных перекрытий.

Нормативные документы

Главное меню

10.7. Вертикальные предельные прогибы элементов конструкций и нагрузки, от которых следует определять прогибы, приведены в табл. 19. Требования к зазорам между смежными элементами приведены в п. 6 рекомендуемого приложения 6.

Вертикальные предельные прогибы f_u

Нагрузки для определения вертикальных прогибов

1. Балки крановых путей под мостовые и подвесные краны, управляемые:

с пола, в том числе тельферы (тали)

От одного крана

из кабины при группах режимов работы (по ГОСТ 25546—82):

Физиологические и технологические

2. Балки, фермы, ригели, прогоны, плиты, настилы (включая поперечные ребра плит и настилов):

а) покрытий и перекрытий, открытых для обзора, при пролете l, м:

Постоянные и временные длительные

б) покрытий и перекрытий при наличии перегородок под ними

Принимаются в соответствии с п. 6 рекомендуемого приложения 6

Приводящие к уменьшению зазора между несущими элементами конструкций и перегородками, расположенными под элементами

в) покрытий и перекрытий при наличии на них элементов, подверженных растрескиванию (стяжек, полов, перегородок)

Действующие после выполнения перегородок, полов, стяжек

г) покрытий и перекрытий при наличии тельферов (талей), подвесных кранов, управляемых:

l/300 или а/150 (меньшее из двух)

Временные с учетом нагрузки от одного крана или тельфера (тали) на одном пути

l/400 или а/200 (меньшее из двух)

От одного крана или тельфера (тали) на одном пути

д) перекрытий, подверженных действию:

Физиологические и технологические

перемещаемых грузов, материалов, узлов и элементов оборудования и других подвижных нагрузок (в том числе при безрельсовом напольном транспорте)

0,7 полных нормативных значений временных нагрузок или нагрузки от одного погрузчика (более неблагоприятное из двух)

нагрузок от рельсового транспорта:

От одного состава вагонов (или одной напольной машины) на одном пути

3. Элементы лестниц (марши, площадки, косоуры), балконов, лоджий

Те же, что в поз. 2, а

Определяются в соответствии с п. 10.10

4. Плиты перекрытий, лестничные марши и площадки, прогибу которых не препятствуют смежные элементы

Сосредоточенная нагрузка 1 кН (100 кгс) в середине пролета

5. Перемычки и навесные стеновые панели над оконными и дверными проемами (ригели и прогоны остекления)

Приводящие к уменьшению зазора между несущими элементами и оконным или дверным заполнением, расположенным под элементами

Те же, что в поз. 2, а

Обозначения, принятые в табл. 19:

l — расчетный пролет элемента конструкции;

а — шаг балок или ферм, к которым крепятся подвесные крановые пути.

Примечания: 1. Для консоли вместо l следует принимать удвоенный ее вылет.

2. Для промежуточных значений l в поз. 2, а предельные прогибы следует определять линейной интерполяцией, учитывая требования п. 7 рекомендуемого приложения б.

3. В поз. 2, а цифры, указанные в скобках, следует принимать при высоте помещений до 6 м включительно.

4. Особенности вычисления прогибов по поз. 2, г указаны в п. 8 рекомендуемого приложения 6.

5. При ограничении прогибов эстетико-психологическими требованиями допускается пролет l принимать равным расстоянию между внутренними поверхностями несущих стен (или колонн).

10.8. Расстояние (зазор) от верхней точки тележки мостового крана до нижней точки прогнутых несущих конструкций покрытий (или предметов, прикрепленных к ним) должно быть не менее 100 мм.

10.9. Прогибы элементов покрытий должны быть такими, чтобы, несмотря на их наличие, был обеспечен уклон кровли не менее 1/200 в одном из направлений (кроме случаев, оговоренных в других нормативных документах).

10.10. Предельные прогибы элементов перекрытый (балок, ригелей, плит), лестниц, балконов, лоджий, помещений жилых и общественных зданий, а также бытовых помещений производственных зданий исходя из физиологических требований следует определять по формуле

(26)

где g — ускорение свободного падения;

р — нормативное значение нагрузки от людей, возбуждающих колебания, принимаемое по табл. 20;

р₁ — пониженное нормативное значение нагрузки на перекрытия, принимаемое по табл. 3 и 20;

q — нормативное значение нагрузки от веса рассчитываемого элемента и опирающихся на него конструкций;

п — частота приложения нагрузки при ходьбе человека, принимаемая по табл. 20;

b — коэффициент, принимаемый по табл. 20.

Формулы для расчета прогиба балки

Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.

При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.

Виды балок

Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.

Деревянные

Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.

Для расчета максимального прогиба следует учитывать:

1. Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
2. Форма поперечного сечения и другие геометрические характеристики.
3. Различные виды нагрузки на материал.

Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.

Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.

Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:

• электросварка;
• заклепки;
• болты, винты и другие виды резьбовых соединений.

Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.

Для проведения расчета балки на прогиб может помочь видео:

Прочность и жесткость балки

Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.

Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.

Существует два основных метода расчета прочности и жесткости:

1. Простой. При использовании данного метода применяется увеличительный коэффициент.
2. Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.

Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.

Расчет на жесткость

Для расчета прочности балки на изгиб применяется формула:

M – максимальный момент, который возникает в балке;

W_n,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.

R_y является расчетным сопротивлением стали при изгибе. Зависит от вида стали.

γ_c представляет собой коэффициент условий работы, который является табличной величиной.

Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:

1. Составление расчетной схемы объекта.
2. Расчет размеров балки и ее сечения.
3. Вычисление максимальной нагрузки, которая воздействует на балку.
4. Определение точки приложения максимальной нагрузки.
5. Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
6. Вычисление значения жесткости или максимально прогиба балки.

Чтобы составить расчетную схему, потребуются такие данные:

• размеры балки, длину консолей и пролет между ними;
• размер и форму поперечного сечения;
• особенности нагрузки на конструкцию и точно ее приложения;
• материал и его свойства.

Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.

Расчет моментов инерции и сопротивления сечения

Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:

Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.

Определение максимальной нагрузки и прогиба

Для точного определения прогиба балки, лучше всего применять данную формулу:

q является равномерно-распределенной нагрузкой;

E – модуль упругости, который является табличной величиной;

I – момент инерции сечения.

Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.

Особенности расчета на прогиб

Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:

1. Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.
2. Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
3. Варианты нагружения консольного стержня, который закреплен жестко.
4. Действие на конструкцию сложной нагрузки.

Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.

Пример подсчета прогиба

Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:

• материал изготовления – древесина;
• плотность составляет 600 кг/м3;
• длина составляет 4 м;
• сечение материала составляет 150*200 мм;
• масса перекрывающих элементов составляет 60 кг/м²;
• максимальная нагрузка конструкции составляет 249 кг/м;
• упругость материала составляет 100 000 кгс/ м²;
• J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:

• вес одного метра балки;
• вес м2 перекрытия;
• расстояние, которое оставляется между балками;
• временная нагрузка;
• нагрузка от перегородок на перекрытие.

Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.

Если подставить все эти значения в формулу, то получится:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].

Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.

Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.

Эти примеры помогут сделать расчет металлической балки без напряга

Металлические балки двутавровые

Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.

Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.

Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.

Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.

Расчет ведется по двум характеристикам – на прочность и на жесткость. По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.

Исходные данные для расчетов

Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали W_y и минимальные моменты инерции J_y.

Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.

Распределенная нагрузка при таком типе плит будет равна 325 кгс / м 2 . К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м 2 ) и возможную временную нагрузку (200 кгс / м 2 ). В итоге нагрузка, распределенная по площади:

Q = 325 + 75 + 200 = 600 кгс / м 2 ,

а линейная нагрузка

q = Q * p = 600 кгс / м = 6 кгс / см.

Эта величина используется в дальнейших расчетах.

Расчет на прогиб

Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).

Искомая величина момента, в таком случае:

M_y = (q * L 2 ) / 8 = 6 * 450 2 / 8 = 151875 кгс * см.

Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см 2 :

W_y = 151875 / 2150 = 70,6 см 3 .

Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см 3) . Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.

Расчет балки на прогиб – формулы и инструкция

В инженерных и инженерно-строительных науках (сопротивление материалов, строительная механика, теория прочности), под балкой понимается элемент несущей конструкции, воспринимающаяся преимущественно на изгибные нагрузки, и имеющая различные формы поперечного сечения.

Конечно, в реальном строительстве, балочные конструкции подвержены и другим видам нагружения (ветровой нагрузке, вибрации, знакопеременному нагружения), однако основной расчет горизонтальных, многоопертых и жесткозакрепленных балок проводится на действие или поперечной, или приведенной к ней эквивалентной нагрузке.

Расчетная схема рассматривает балку как жесткозакрепленный стержень или как стержень, установленный на двух опорах. При наличии 3 и более опор, стержневая система считается статически неопределимой и расчет на прогиб как всей конструкции, так и ее отдельных элементов, значительно усложняется.

При этом, основное нагружение рассматривается как сумма сил, действующая в направлении перпендикулярному сечению. Целью расчета на прогиб является определение максимального прогиба (деформации) который не должен превышать предельных значений и характеризует жесткость как отдельного элемента (так и всей связанной с ней строительной конструкции.

Основные положения расчетных методик

Современные строительные методики расчета стержневых (балочных) конструкций на прочность и жесткость, дают возможность уже на стадии проектирования определить значение прогиба и сделать заключение о возможности эксплуатации строительной конструкции.

Расчет на жесткость позволяет решить вопрос о наибольших деформациях, которые могут возникнуть в строительной конструкции при комплексном действии различного вида нагрузок.

Современные методы расчета, проводимые с использованием специализированных расчетов на электронно-вычислительных машинах, или выполняемые при помощи калькулятора, позволяют определить жесткость и прочность объекта исследований.

Несмотря на формализацию расчетных методик, которые предусматривают использование эмпирических формул, а действие реальных нагрузок учитывается введением поправочных коэффициентов (коэффициенты запаса прочности), комплексный расчет достаточно полно и адекватно оценивает эксплуатационную надежность возведенного сооружения или изготовленного элемента какой-либо машины.

Несмотря на отдельность прочности расчетов и определения жесткости конструкции, обе методики взаимосвязаны, а понятия «жесткость» и «прочность» неразделимы. Однако, в деталях машин, основное разрушение объекта происходит из-за потери прочности, в то время как объекты строительной механики часто непригодны к дальнейшей эксплуатации из значительных пластических деформаций, которые свидетельствуют о низкой жесткости элементов конструкции или объекта в целом.

Сегодня, в дисциплинах «Сопротивление материалов», «Строительная механика» и «Детали машин», приняты два метода расчета на прочность и жесткость:

1. Упрощенный (формальный), при проведении которого в расчетах применяются укрупненные коэффициенты.
2. Уточненный, где используются не только коэффициенты запаса прочности, но и производится расчет контракции по предельным состояниям.

Алгоритм расчета на жесткость

Формула определения прочности балки на изгиб

Где:

• M – максимальный момент, возникающий в балке (находится по эпюре моментов);
• W_n,min – момент сопротивления сечения (находится по таблице или вычисляется для данного профиля), у сечения обычно 2-а момента сопротивления сечения, в расчетах используется Wx, если нагрузка перпендикулярна оси х-х профиля или Wy, если нагрузка перпендикулярна оси y-y;
• R_y– расчетное сопротивление стали при изгибе (задается в соответствии с выбором стали);
• γ_c – коэффициент условий работы (данный коэффициент можно найти в таблице 1 СП 16.13330.2011;

Алгоритм расчета на жесткость (определение величины прогиба) достаточно формализован и не представляет труда для овладения.

Для того, чтобы определить прогиб балки, необходимо в нижеприведенной последовательности выполнить следующие действия:

1. Составить расчетную схему объекта исследований.
2. Определить размерные характеристики балки и расчетных сечений.
3. Рассчитать максимальную нагрузку, действующую на балку, определив точку ее приложения.
4. При необходимости, балка (в расчетной схеме она заменятся невесомым стержнем) дополнительно проверяется на прочность по максимальному изгибающему моменту.
5. Определяется значение максимального прогиба, который характеризует жесткость балки.

Для составления расчетной схемы балки, необходимо знать:

1. Геометрические размеры балки, включая пролет между опорами, а при наличии консолей – их длину.
2. Геометрическую форму и размеры поперечного сечения.
3. Характер нагрузки и точки их приложения.
4. Материал балки и его физико-механические характеристики.

При простейшем расчете двухопорных балок, одна опора считается жесткой, а вторая закреплена шарнирно.

Определение моментов инерции и сопротивления сечения

К геометрическим характеристикам, которые необходимы при выполнении расчетов на прочность и жесткость, относится момент инерции сечения (J) и момент сопротивления (W). Для вычисления их величины существуют специальные расчётные формулы.

Формула момента сопротивления сечения

Определение максимальной нагрузки и прогиба

Формула определения прогиба

Где:

• q – равномерно-распределенная нагрузка, выраженная в кг/м (Н/м);
• l – длина балки в метрах;
• E – модуль упругости (для стали равен 200-210 ГПа);
• I – момент инерции сечения.

При определении максимальной нагрузки, необходимо учитывать довольно значительное число факторов, действующих как постоянно (статические нагрузки), так и периодически (ветровая, вибрационная ударная нагрузка).

В одноэтажном доме, на деревянный брус потолочного перекрытия будут действовать постоянные весовые усилия от собственного веса, расположенных на втором этаже простенков, мебели, находящихся обитателей и так далее.

Особенности расчета на прогиб

Конечно, расчет элементов перекрытий на прогиб проводится для всех случаев и обязателен при наличии значительного уровня внешних нагрузок.

Сегодня, все вычисления величины прогиба достаточно формализованы и все сложные реальные нагружения сведены к следующим простым расчетным схемам:

1. Стержень, опирающийся на неподвижную и шарнирно закрепленную опоры, воспринимающий сосредоточенную нагрузку (случай рассмотрен выше).
2. Стержень, опирающийся на неподвижную и шарнирно закрепленную на который действует распределенное нагружение.
3. Различные варианты нагружения жестко закрепощённого консольного стержня.
4. Действие на расчетный объект сложной нагрузки – распределенной, сосредоточенной, изгибающего момента.

При этом, методика и алгоритм расчета не зависят от материала изготовления, прочностные характеристики которого учтены различными значениями модуля упругости.

Разновидности балок, применяемых в строительстве

Современная стройиндустрия при возведении сооружений промышленного и жилого назначения, практикует использование стержневых систем различного сечения, формы и длины, изготовленных из различных материалов.

Наиболее большее распространение получили стальные и деревянные изделия. В зависимости от используемого материала, определение значения прогиба имеет свои нюансы, связанные со структурой и однородностью материала.

Деревянные

Современное малоэтажное строительство индивидуальных домов и загородных коттеджей практикует широкое использование лаг, изготовленных из хвойных и твердых пород древесины.

В основном, деревянные изделия, работающие на изгиб, применяются для обустройства напольных и потолочных перекрытий. Именно эти элементы конструкции испытают наибольшее действие поперечных нагрузок, взывающих наибольший прогиб.

Стрела прогиба деревянной лаги зависит:

1. От материала (породы древесины), который использовался при изготовлении балки.
2. От геометрических характеристик и формы попечённого сечения расчетного объекта.
3. От совокупного действия различного вида нагрузок.

Критерий допустимости прогиба балки учитывает два фактора:

1. Соответствие реального прогиба предельно допустимым значениям.
2. Возможность эксплуатации конструкции при наличии расчетного прогиба.

Имеют более сложное сечение, которое может быть составным, выполненным из нескольких видов металлического проката. При расчете металлоконструкций, помимо определения жесткости самого объекта его элементов, часто появляется необходимость определения прочностных характеристик соединений.

Обычно, соединение отдельных элементов стальной металлоконструкции проводится:

1. С использованием электросварки.
2. Путем применения резьбовых (шпилечных, болтовых и винтовых) соединений.
3. Соединением заклепками.