Модуль сдвига меди

Модуль сдвига меди

Лабораторная работа № 5 определение модуля сдвига из деформации кручения

Проверить справедливость закона Гука для деформации кручения.

Измерить модуль сдвига металла.

Теоретическое введение

Изменение формы и размеров тела под действием внешних сил называется деформацией. При деформации в теле возникают силы упругости, которые стремятся восстановить первоначальные размеры и форму тела. Величину этих сил принято характеризовать напряжением – величиной, численно равной силе, действующей на единицу площади сечения тела.

Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Если этого не происходит, говорят о пластической деформации. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются остаточными.

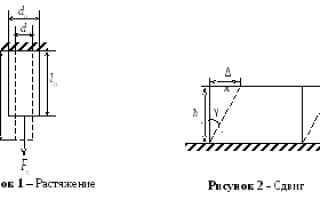
Основными видами деформаций являются растяжение (сжатие) (рисунок 1) и сдвиг (рисунок 2). Все остальные деформации (изгиб, кручение и другие) можно свести к этим основным видам.

Рассмотрим деформацию растяжения на примере однородного стержня. Пусть один конец стержня закреплен, а к другому концу приложена сила, перпендикулярная поперечному сечению стержня (рисунок 1). Под действием этой силы стержень удлиняется на Δl = l — l . Эта величина называется абсолютным удлинением. Для количественной характеристики величины деформации обычно используют относительное удлинение . При деформации растяжения в теле возникаетнормальное напряжение . При малых деформациях справедлив закон Гука: возникающее в теле напряжение прямо пропорционально величине деформации:

,

где коэффициент пропорциональности E называется модулем Юнга. Эта величина является характеристикой упругих свойств материала тела по отношению к деформации растяжения (сжатия).

Деформацию сдвига проще всего наблюдать, если взять брусок, имеющий форму прямоугольного параллелепипеда (рисунок 2) и приложить к нему силу , направленную по касательной к его верхней грани (нижняя грань бруска закреплена). Под действием этой силы горизонтальные слои тела смещаются в направлении приложенной силы, причем расстояние между ними не изменяется. Величина деформации сдвига характеризуется углом сдвига γ. В теле при этом возникает касательное напряжение, гдеS – площадь поверхности, к которой приложена сила. Закон Гука для деформации сдвига может быть записан в виде

,

где G – модуль сдвига (характеристика упругих свойств материала тела по отношению к деформации сдвига).

Модуль упругости разных материалов, включая сталь

Перед тем, как использовать какой-либо материал в строительных работах, следует ознакомиться с его физическими характеристиками для того, чтобы знать как с ним обращаться, какое механическое воздействие будет для него приемлемым, и так далее. Одной из важных характеристик, на которые очень часто обращают внимание, является модуль упругости.

Ниже рассмотрим само понятие, а также эту величину по отношению к одному из самых популярных в строительстве и ремонтных работах материалу — стали. Также будут рассмотрены эти показатели у других материалов, ради примера.

Модуль упругости — что это?

Модулем упругости какого-либо материала называют совокупность физических величин, которые характеризуют способность какого-либо твёрдого тела упруго деформироваться в условиях приложения к нему силы. Выражается она буквой Е. Так она будет упомянута во всех таблицах, которые будут идти далее в статье.

Невозможно утверждать, что существует только один способ выявления значения упругости. Различные подходы к изучению этой величины привели к тому, что существует сразу несколько разных подходов. Ниже будут приведены три основных способа расчёта показателей этой характеристики для разных материалов:

• Модуль Юнга (Е) описывает сопротивление материала любому растяжению или сжатию при упругой деформации. Определяется вариант Юнга отношением напряжения к деформации сжатия. Обычно именно его называют просто модулем упругости.
• Модуль сдвига (G), называемый также модулем жёсткости. Этот способ выявляет способность материала оказывать сопротивление любому изменению формы, но в условиях сохранения им своей нормы. Модуль сдвига выражается отношением напряжения сдвига к деформации сдвига, которая определяется в виде изменения прямого угла между имеющимися плоскостями, подвергающимися воздействию касательных напряжений. Модуль сдвига, кстати, является одной из составляющих такого явления, как вязкость.
• Модуль объёмной упругости (К), которые также именуется модулем объёмного сжатия. Данный вариант обозначает способность объекта из какого-либо материала изменять свой объём в случае воздействия на него всестороннего нормального напряжения, являющимся одинаковым по всем своим направлениям. Выражается этот вариант отношением величины объёмного напряжения к величине относительного объёмного сжатия.
• Существуют также и другие показатели упругости, которые измеряются в других величинах и выражаются другими отношениями. Другими ещё очень известными и популярными вариантами показателей упругости являются параметры Ламе или же коэффициент Пуассона.

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

• Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
• Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
• Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
• Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
• Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
• Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
• И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Модуль сдвига меди

Модуль упругости (Модуль Юнга)

Если на изделие из определенного материала воздействовать некой силой, то он начинает сопротивляться этому действию: сжиматься, растягиваться или изгибаться. Способность к такому противостоянию можно оценить и выразить математически. Название этой прочностной характеристики – модуль упругости.

Параметр для каждого материала различный, и характеризует его прочность. Пользуются величиной при разработке конструкций, деталей и других изделий, с целью предотвращения нарушения их целостности.

Общее понятие

При любом внешнем воздействии на предмет, внутри его возникают встречные силы, компенсирующие внешние. Для идеальных систем, находящихся в равновесии, силы равномерно распределены и равны, что позволяет сохранить форму предмета. Реальные системы не подчиняются таким правилам, что может привести к их деформации. Оценивая прочность материалов, говорят об их упругости.

Определение модуля Юнга твердых тел

Упругие материалы – это те, которые после прекращения внешнего воздействия, восстанавливают свою первоначальную форму.

Внутренние силы распределены равномерно по всей площади поперечного сечения предмета, имеют свою интенсивность, которая выражается количественно, называется напряжением (р) и измеряется в Н/м2 или по международной системе Па.

Напряжение имеет свою пространственную направленность: перпендикулярно площади сечения предмета – нормальное напряжение (σz) и лежащая в плоскости сечения – касательное напряжение (τz).

Опыт с пружинными весами

Модуль упругости (Е) как единицу измерения отношения материала к линейной деформации, и нормальное напряжение связывает формула закона Гука:

где ε – относительное удлинение или деформация.

Преобразовав формулу (1) для выражения из нее нормального напряжения, можно увидеть, что Е является постоянной при относительном удлинении, и называется коэффициентом жесткости, а его единицы измерения Па, кгс/мм2 или Н/м2:

Модуль упругости – это единица измерения отношения напряжения, создаваемого в материале, к линейной деформации, такой как, растяжение и сжатие.

В справочных материалах размерность модуля упругости выражается в МПа, так как деформация имеет довольно малое значение. А зависимость между этими величинами обратно пропорциональная. Таким образом, Е имеет высокое значение, определяемое 107-109.

Способы расчета модуля упругости

Известны также и другие характеристики упругости, которые описывают сопротивление материалов к воздействиям как к линейным, так и отличным от них.

Величина, которая характеризует сопротивление материала к растяжению, то есть увеличению его длины вдоль оси, или к сжатию – сокращению линейного размера, называется модулем продольной упругости.

Обозначается как Е и выражается в Па или ГПа.

Показывает зависимость относительного удлинения от нормальной составляющей cилы (F) к ее площади распространения (S) и упругости (Е):

Параметр также называют модулем Юнга или модулем упругости первого рода, в таблице показаны величины для материалов различной природы.

Модулем упругости второго рода называют модуль сдвига (G), который показывает сопротивление материала к сдвигающей силе (FG). Может быть выражена двумя способами.

• Через касательные напряжения (τz) и угол сдвига (γ):

• Через соотношение модуля упругости первого рода и коэффициента Пуасонна (ν):

Определенное в результате экспериментов значение сопротивления материала изгибу, называется модулем упругости при изгибе, и вычисляется следующим образом:

EИ = ((0,05-0,1)Fр— 0,2Fр)L2 / 4bh3(ƒ2-ƒ1) (6)

где Fр – разрушающая сила, Н;

L – расстояние между опорами, мм;

b, h – ширина и толщина образца, мм;

ƒ1, ƒ2– прогибы, образованные в результате нагрузки F1 и F2.

При равномерном давлении по всему объему на объект, возникает его сопротивление, называемое объемным модулем упругости или модулем сжатия (К). Выразить этот параметр можно, практически через все известные модули и коэффициент Пуассона.

Определение модуля упругости щебеночного основания

Параметры Ламе также используют для описания оценки прочности материала. Их два μ – модуль сдвига и λ. Они помогают учитывать все изменения внутри материала в трехмерном пространстве, тогда соотношения между нормальным напряжением и деформацией будет выглядеть следующим образом:

σ = 2με + λtrace(ε)I (7)

Оба параметра могут быть выражены из следующих соотношений:

Модуль упругости различных материалов

Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:

• природы веществ, формирующих состав материала;
• моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
• структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
• плотности материала (распределения частиц в его объеме);
• обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).

Так, например, в справочных данных можно найти, что модуль упругости для алюминия составляет диапазон от 61,8 до 73,6 ГПа. Видимо, это и зависит от состояния металла и вида обработки, потому как для отожженного алюминия модуль Юнга – 68,5 ГПа.

Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:

• бронза – 10,4 ГПа;
• алюминиевая бронза при литье – 10,3 ГПа;
• фосфористая бронза катанная – 11,3 ГПа.

Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.

Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:

• литая – 82 ГПа;
• прокатанная – 108 ГПа;
• деформированная – 112 ГПа;
• холоднотянутая – 127 ГПа.

Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.

Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.

Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.

Модули упругости некоторых материалов

На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:

Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.

Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.

Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.

Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

1. по справочным данным из таблиц;
2. экспериментальными методами для небольшого образца;
3. расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки.

Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность.

При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Модуль сдвига — Shear modulus

В науке материалов , модуль сдвига или модулем жесткости , обозначаемой G , или иногда S или ц , определяется как отношение напряжения сдвига к деформации сдвига :

г знак равно d е е τ Икс Y γ Икс Y знак равно F / A Δ Икс / L знак равно F L A Δ Икс < Displaystyle G < stackrel < mathrm <Защиту>> <=>> < гидроразрыва < тау _ <ху>> < Gamma _ <ху>>> = < гидроразрыва < дельта х / л>> = < гидроразрыва <А дельта х>>>

τ Икс Y знак равно F / A < Displaystyle тау _ <ху>= F / A > = Напряжение сдвига F < Displaystyle F> это сила, которая действует A < Displaystyle A> это область, на которой сила действует γ Икс Y < Displaystyle Gamma _ <ху>> = Деформации сдвига. В технике , в другом месте знак равно Δ Икс / L знак равно загар ⁡ θ < Displaystyle: = дельта х / л = загар тета> знак равно θ < Displaystyle: = Theta> Δ Икс < Displaystyle Delta х> это поперечное смещение L < Displaystyle л> начальная длина

Полученный СИ единица модуля сдвига является паскалем (Па), хотя это обычно выражается в гигапаскаль (ГП) или в тысячах фунтов на квадратный дюйм (кг на квадратный дюйм) . Ее мерная форма есть М 1 л -1 Т -2 , заменив силы на массы раз ускорения .

содержание

объяснение

Модуль сдвига является одной из нескольких величин для измерения жесткости материалов. Все они возникают в обобщенном законе Гука :

• Модуль ЮнгаЕ описывает реакцию деформации материала к одноосной деформации в направлении этого напряжения (например , потянув за концы проволоки или положить вес на верхнюю часть колонки, с проволокой , получить больше и колонку потери высоты),
• в коэффициент Пуассонаν описывает отклик в направлениях , ортогональных к этому одноосного напряжения (провод становится тоньше и толще столбец),
• объемный модуль упругостиК описывает реакцию материала к (однородной) гидростатического давления (например , давление на дне океана или глубокий бассейн),
• модуль сдвигаG описывает отклик материала на напряжение сдвига (как резка его с тупыми ножницами).
• Эти модули не являются независимыми, и для изотропных материалов они связаны через уравнение . 2 г ( 1 + ν ) знак равно Е знак равно 3 К ( 1 — 2 ν ) < Displaystyle 2G (1+ Nu) = Е = 3K (1-2 Nu)>

Модуль сдвига связан с деформацией твердого тела , когда он испытывает усилие параллельно одной из его поверхностей , а ее противоположная поверхность испытывает противодействующую силу (например, трение). В случае объекта формы , как прямоугольная призма, он будет деформироваться в параллелепипед . Анизотропные материалы , такие как древесины , бумаги , а также по существу всех кристаллов обладают одного различной реакцию на стресс материала или деформации при испытании в разных направлениях. В этом случае, один , возможно , потребуется использовать полный тензор-выражение упругих констант, а не одно скалярное значение.

Одним из возможного определения жидкости будет материалом с нулевым модулем сдвига.

В однородных и изотропных твердых телах, существует два вида волн, волны давления и сдвиговых волн . Скорость волны сдвига, управляются модулем сдвига, ( v s ) < Displaystyle (V_ )>

Читать еще:  Как сделать пантограф своими руками

v s знак равно г ρ < Displaystyle V_ = < SQRT < гидроразрыва < Rho>>>>

G представляет собой модуль сдвига ρ < Displaystyle Rho> телесная — й плотность .

Модуль сдвига металлов

Модуль сдвига металлов, как правило, наблюдается уменьшение с ростом температуры. При высоких давлениях, модуль сдвига также, как представляется, возрастает с увеличением приложенного давления. Корреляция между температурой плавления, энергией образования вакансий и модулем сдвига наблюдались во многих металлах.

Несколько моделей существуют, что попытка предсказать модуль сдвига металлов (и, возможно, что сплавы). Shear модель модуля упругости, которые были использованы в пластиковых вычислениях потока включает в себя:

1. модель модуля сдвига МТС разработана и использован в сочетании с механическим Пороговым усилием модели напряжения пластического течения (МТС).
2. Стейнберг-Кокрэн-Гуинан (СКГ) Модель модуля сдвига разработана и использован в сочетании с Steinberg-Cochran-Гуинан-Лунд (SCGL) поток модели стресса.
3. Надаль и LePoac (NP) , модуль упругости при сдвиге модель , которая использует теорию Lindemann для определения зависимости температуры и модели SCG для зависимости давления от модуля сдвига.

Модель модуля сдвига МТС

Модель модуля сдвига МТС имеет вид:

μ ( T ) знак равно μ 0 — D ехр ⁡ ( T 0 / T ) — 1 < Displaystyle му (Т) = му _ <0>— < гидроразрыва < ехр (Т_ <0>/ Т) -1>>>

где представляет собой модуль сдвига при , а и материальные константы. μ 0 < Displaystyle мю _ <0>> T знак равно 0 К < Displaystyle Т = 0K> D < Displaystyle D> T 0 < Displaystyle T_ <0>>

Модель модуля сдвига СКГ

Steinberg-Кокрэн-Гуинан (СКГ) Модель модуля сдвига зависит от давления и имеет вид

μ ( п , T ) знак равно μ 0 + ∂ μ ∂ п п η 1 / 3 + ∂ μ ∂ T ( T — 300 ) ; η знак равно ρ / ρ 0 < Displaystyle му (р, Т) = му _ <0>+ < гидроразрыва < парциальное му>< парциальное р>> < гидроразрыва <р>< ETA ^ <1/3>>> + < гидроразрыва < парциального му>< парциальный Т>> (Т-300); четырехъядерного ETA: = Rho / Rho _ <0>>

где ц модуль сдвига в опорном состоянии ( Т = 300 К, р = 0, η = 1), р представляет собой давление, а Т представляет собой температуру.

Модель NP модуля сдвига

Надаль-Ле Poac (НП) Модель модуля сдвига представляет собой модифицированный вариант модели SCG. Эмпирическая температурная зависимость модуля сдвига в модели SCG заменяется уравнением на основе теории плавления Lindemann . Модель модуля сдвига НП имеет вид:

Т вправо]; четырехъядерных C: = < cfrac <(6 пи ^ <2>) ^ <2/3>> <3>> <е ^ 2>>

J ( T ^ ) знак равно 1 + ехр ⁡ [ — 1 + 1 / ζ 1 + ζ / ( 1 — T ^ ) ] за T ^ знак равно T T м ∈ [ 0 , 1 + ζ ] , < Displaystyle < mathcal > (< <шлем Т>>): = 1+ ехр влево [- < cfrac <1 + 1 / дзета><1+ дзета / (1- < шляпы >)>> право] четырехъядерных < текст <для>> четырехъядерных < шляпы >: = < гидроразрыва <Т><Т_ <т>>> в [0, 1+ дзета]>

и μ является модулем сдвига при 0 К и давлении окружающей среды, ζ представляет собой материал , параметр, к _б является постоянной Больцмана , т является атомной массой , а е является постоянная Линдеманном .

Модуль сдвига меди

ГОСТ 33843-2016
(ISO 15310:1999)

Метод определения модуля сдвига в плоскости методом кручения

Polymer composites. Method for determination of shear modulus in the plane by torsion

Дата введения 2017-07-01

Цели, основные принципы и порядок проведения работ по межгосударственной стандартизации установлены в ГОСТ 1.0-2015 «Межгосударственная система стандартизации. Основные положения» и ГОСТ 1.2-2015 «Межгосударственная система стандартизации. Стандарты межгосударственные, правила и рекомендации по межгосударственной стандартизации. Правила разработки, принятия, обновления и отмены»

Сведения о стандарте

1 ПОДГОТОВЛЕН Федеральным государственным унитарным предприятием «Всероссийский научно-исследовательский институт стандартизации материалов и технологий» (ФГУП «ВНИИ СМТ») совместно с Открытым акционерным обществом «НПО Стеклопластик» (ОАО «НПО Стеклопластик») при участии Объединения юридических лиц «Союз производителей композитов» (Союзкомпозит) и Автономной некоммерческой организацией «Центр нормирования, стандартизации и классификации композитов» (АНО «Стандарткомпозит») на основе собственного перевода на русский язык англоязычной версии стандарта, указанного в пункте 4

2 ВНЕСЕН Федеральным агентством по техническому регулированию и метрологии

3 ПРИНЯТ Межгосударственным советом по стандартизации, метрологии и сертификации (протокол от 28 июня 2016 г. N 49)

За принятие проголосовали:

Краткое наименование страны по МК (ИСО 3166) 004-97

Сокращенное наименование национального органа по стандартизации

Госстандарт Республики Беларусь

4 Приказом Федерального агентства по техническому регулированию и метрологии от 20 октября 2016 г. N 1438-ст межгосударственный стандарт ГОСТ 33843-2016 (ISO 15310:1999) введен в действие в качестве национального стандарта Российской Федерации с 1 июля 2017 г.

5 Настоящий стандарт является модифицированным по отношению к международному стандарту ISO 15310:1999* «Материалы композиционные пластмассовые, армированные волокном. Определение модуля упругости при сдвиге в плоскости с применением метода кручения плиты» («Fibre-reinforced plastic composites — Determination of the in-plane shear modulus by the plate twist method», MOD).
________________
* Доступ к международным и зарубежным документам, упомянутым в тексте, можно получить, обратившись в Службу поддержки пользователей. — Примечание изготовителя базы данных.

Ссылки на международные стандарты, которые приняты в качестве межгосударственных стандартов, заменены в разделе «Нормативные ссылки» и тексте стандарта ссылками на соответствующие межгосударственные стандарты и выделены курсивом*.
________________
* В бумажном оригинале обозначения и номера стандартов и нормативных документов в разделах «Предисловие», 9 «Протокол испытаний», п.5.1.2, приложениях ДБ и ДВ приводятся обычным шрифтом, остальные по тексту документа выделены курсивом. — Примечание изготовителя базы данных.

Содержание исключенного раздела 11 приведено в дополнительном приложении ДА.

Наименование настоящего стандарта изменено относительно наименования международного стандарта в целях соблюдения принятой терминологии.

Сравнение структуры настоящего стандарта со структурой примененного международного стандарта приведено в дополнительном приложении ДБ.

Разъяснение причин изменения структуры приведено в примечаниях в приложении ДБ.

Официальный экземпляр международного стандарта, на основе которого подготовлен настоящий межгосударственный стандарт, и международных стандартов, на которые даны ссылки, имеются в Федеральном агентстве по техническому регулированию и метрологии.

Сведения о соответствии ссылочных межгосударственных стандартов международным стандартам, использованным в качестве ссылочных в примененном международном стандарте, приведены в дополнительном приложении ДВ

6 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодном информационном указателе «Национальные стандарты», а текст изменений и поправок — в ежемесячном информационном указателе «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячном информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет (www.gost.ru)

1 Область применения

1 Область применения

Настоящий стандарт распространяется на полимерные композиты и устанавливает метод определения модуля сдвига в плоскости методом кручения. Если данный метод применяют к изотропным материалам, то измеренный модуль упругости при сдвиге не зависит от направления сдвига.

Данный метод применим к композитам, армированным волокном, как с термореактивной матрицей, так и с термопластичной матрицей.

Данный метод не применим для определения прочности на сдвиг.

Слоистые материалы с разными формами волокон и(или) с разными направлениями волокон и структурой слоев должны иметь равномерность армирующих элементов по толщине.

Главные оси материала при их наличии должны иметь направление под прямым углом к краям плиты (см. 3.8).

Данный метод применим к образцам, изготовленным путем литья под установленные габаритные размеры или вырезанным механически из пластин для испытаний или плоских участков изделий.

2 Нормативные ссылки

В настоящем стандарте использованы нормативные ссылки на следующие стандарты*:
________________
* Таблицу соответствия национальных стандартов международным см. по ссылке. — Примечание изготовителя базы данных.

ГОСТ 33345-2015 (ISO 1268-1:2005) Композиты полимерные. Производство пластин для изготовления образцов для испытаний. Общие технические требования

ГОСТ 33347-2015 (ISO 1268-3:2005) Композиты полимерные. Производство пластин прессованием для изготовления образцов для испытаний

ГОСТ 33350-2015 (ISO 1268-7:2005) Композиты полимерные. Производство пластин литьевым прессованием для изготовления образцов для испытаний

ГОСТ 166-89 (ИСО 3599-76) Штангенциркули. Технические условия

ГОСТ 6507-90 Микрометры. Технические условия

ГОСТ 12423-2013 (ISO 291:2008) Пластмассы. Условия кондиционирования и испытания образцов (проб)

ГОСТ 28840-90 Машины для испытания материалов на растяжение, сжатие и изгиб. Общие технические требования

Примечание — При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования — на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодному информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по выпускам ежемесячного информационного указателя «Национальные стандарты» за текущий год. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3 Термины и определения

В настоящем стандарте применены следующие термины с соответствующими определениями:

3.1 упругая деформация плиты (пластины) w, мм: Расстояние, которое проходят точки нагружения относительно точек опор (рисунок 1).

Рисунок 1 — Принцип испытания

Рисунок 1 — Принцип испытания

3.2 толщина образца h, мм: Среднее значение толщины образца.

Читать еще:  Как очистить медь от изоляции

3.3 модуль упругости при сдвиге в плоскости, модуль сдвига в плоскости G , ГПа: Модуль упругости при сдвиге изотропных материалов в направлении, отличном от направления материала армирования, данную величину измеряют в пределах упругой деформации плиты на интервале 0,1h и 0,3h.

3.4 скорость проведения испытаний, мм/мин: Темп движения нагружающих элементов относительно точек опоры.

3.5 пролет S, мм: Среднее расстояние S между двумя точками опоры и расстояние S между двумя точками нагружения (рисунок 2).

Рисунок 2 — Позиции точек опоры и точек нагружения

+ — точка опоры; O — точка нагружения

Рисунок 2 — Позиции точек опоры и точек нагружения

3.6 длина в поперечном сечении D, мм: Расстояние между диаметрально противоположными углами плиты, которое вычисляют по формуле

где , — средняя ширина образца в каждом направлении, мм.

3.7 значения ширины образцов , , мм: Средние значения ширины образца в каждом направлении (см. рисунок 1).

3.8 координатные оси образца: Координатные оси испытуемого материала, как указано на рисунке 3.

Примечание — Направление, которое параллельно главной оси волокон, указано как «направление 1», а направление, которое перпендикулярно данной оси, а также в плоскости волокон — как «направление 2». «Направление 1» также называется направлением под нулевым (0°) углом или продольным направлением, а «направление 2» — направлением под прямым (90°) углом или поперечным направлением. Аналогичное определение используют по отношению к материалу с предпочтительной укладкой волокон и в тех случаях, когда направление (например, длина) имеет отношение к процессу изготовления.

Рисунок 3 — Оси симметрии для материала, армированного волокном

Рисунок 3 — Оси симметрии для материала, армированного волокном

4 Сущность метода

Образец для испытания имеет опору в двух точках. Опоры размещают в непосредственной близости к противоположным углам по диагонали плиты. Плита испытывает упругую деформацию при постоянстве скорости нагружения с двух точек, находящихся на противоположной диагонали (см. рисунок 1), до момента набора образцом для испытаний заданной деформации. Общее усилие в точках нагружения измеряют как зависимость упругой деформации от точек нагружения.

5 Аппаратура

5.1 Машина для испытаний по ГОСТ 28840, обеспечивающая нагружение образца с заданной постоянной скоростью (1±0,2) мм/мин.

5.1.1 Точки опоры и точки нагружения

Две точки опоры и две точки нагружения устанавливают таким образом, как указано на рисунке 2. Точки опоры и точки нагружения должны регулироваться с точностью до 0,5 мм от требуемого положения.

Точки опоры и нагружения монтируют на жесткой траверсе, при этом траверсы устанавливают перпендикулярно друг к другу. Точки нагружения перемещают в соответствии с их креплением к жесткой траверсе одновременно и равным образом относительно точек неподвижных опор.

Примечание — Рекомендуемая конструкция для точек опоры и нагружения указана на рисунке 4.

Радиус r точек опоры и нагружения должен быть (2,0±0,2) мм (см. рисунок 4). Рекомендуемое значение высоты конуса H составляет 20 мм, а радиуса основной окружности R — 10 мм.

Рисунок 4 — Предлагаемая конструкция точек опоры и нагружения

Рисунок 4 — Предлагаемая конструкция точек опоры и нагружения

5.1.2 Индикаторы нагрузки и упругой деформации, погрешность измерения которых не должна превышать ±2% от погрешности максимального значения шкалы (см. ГОСТ 33345).

Примечание — При использовании движения траверсной головки для измерений упругой деформации плиты рекомендуется выполнить поправку на изменение направления комплекса нагружения (т.e. погрешности, которые происходят по причине всех добавочных упругих деформаций, например смещений в аппарате для испытаний, изгиба опорной балки, смещения по датчику нагрузки и местного вдавливания).

5.2 Микрометры и штангенциркули

5.2.1 Микрометры по ГОСТ 6507, обеспечивающие измерение толщины с точностью ±0,01 мм.

5.2.2 Штангенциркули по ГОСТ 166, обеспечивающие измерение ширины с точностью 0,1 мм.

6 Подготовка к проведению испытаний

6.1 Образцы для испытаний

6.1.1 Форма и размеры

Образцы для испытаний должны быть квадратными и плоскими.

6.1.1.1 Образец в виде пластины

Основные параметры образца в виде пластины представлены в таблице 1.

Модуль Юнга (упругости)

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Основные сведения

Модуль Юнга, (называемый также модулем продольной упругости и модулем упругости первого рода) это важная механическая характеристика вещества. Он является мерой сопротивляемости продольным деформациям и определяет степень жесткости. Он обозначается как E; измеряется н/м 2 или в Па.

Это важный коэффициент применяют при расчетах жесткости заготовок, узлов и конструкций, в определении их устойчивости к продольным деформациям. Вещества, применяемые для изготовления промышленных и строительных конструкций, имеют, как правило, весьма большие значения E. И поэтому на практике значения Е для них приводят в гигаПаскалях (10 12 Па)

Величину E для стержней поддается расчету, у более сложных конструкций она измеряется в ходе опытов.

Приближенные величины E возможно узнать из графика, построенного в ходе тестов на растяжение.

График теста на растяжение

E- это частное от деления нормальных напряжений σ на относительное удлинение ε.

Закон Гука также можно сформулировать и с использованием модуля Юнга.

Физический смысл модуля Юнга

Во время принудительного изменения формы предметов внутри них порождаются силы, сопротивляющиеся такому изменению, и стремящиеся к восстановлению исходной формы и размеров упругих тел.

Если же тело не оказывает сопротивления изменению формы и по окончании воздействия остается в деформированном виде, то такое тело называют абсолютно неупругим, или пластичным. Характерным примером пластичного тела является брусок пластилина.

Р. Гук исследовал удлинение стрежней из различных веществ, под воздействием подвешенных к свободному концу гирь. Количественным выражением степени изменения формы считают относительное удлинение, равное отношению абсолютного удлинения и исходной длины.

В результате серии опытов было установлено, что абсолютное удлинение пропорционально с коэффициентом упругости исходной длине стрежня и деформирующей силе F и обратно пропорционально площади сечения этого стержня S:

Величину, обратную α, и называют модулем Юнга:

ε = (Δl) / l = α * (F/S)

Отношение растягивающей силы F к S называют упругим напряжением σ:

Закон Гука, записанный с использованием модуля Юнга, выглядит так:

Теперь можно сформулировать физический смысл модуля Юнга: он соответствует напряжению, вызываемому растягиванием стержнеобразного образца вдвое, при условии сохранения целостности.

В реальности подавляющее большинство образцов разрушаются до того, как растянутся вдвое от первоначальной длины. Значение E вычисляют с помощью косвенного метода на малых деформациях.

Коэффициент жёсткости при упругой деформации стержня вдоль его оси k = (ES) / l

Модуль Юнга определяет величину потенциальной энергии тел или сред, подвергшихся упругой деформации.

Значения модуля юнга для некоторых материалов

В таблице показаны значения E ряда распространенных веществ.

Модуль продольной упругости стали вдвое больше модуля Юнга меди или чугуна. Модуль Юнга широко применяется в формулах прочностных расчетов элементов конструкций и изделий в целом.

Предел прочности материала

Это предел возникающего напряжения, после которого образец начинает разрушаться.

Статический предел прочности измеряется при продолжительном приложении деформирующего усилия, динамический — при кратковременном, ударном характере такого усилия. Для большинства веществ динамический предел больше, чем статический.

Инструмент для определения предела прочности

Кроме того, существуют пределы прочности на сжатие материала и на растяжение. Они определяются на испытательных стенда опытным путем, при растягивании или сжатии образцов мощными гидравлическим машинами, снабженными точными динамометрами и измерителями давления. В случае невозможности достижения требуемого давления гидравлическим способом иногда применяют направленный взрыв в герметичной капсуле.

Допускаемое механическое напряжение в некоторых материалах при растяжении

Из жизненного опыта известно, что разные материалы по-разному сопротивляются изменению формы. Прочностные характеристики кристаллических и других твердых тел определяются силами межатомного взаимодействия. По мере роста межатомных расстояний возрастают и силы, притягивающие атомы друг к другу. Эти силы достигают максимума при определенной величине напряжения, равной приблизительно одной десятой от модуля Юнга.

Испытание на растяжение

Эту величину называют теоретической прочностью, при ее превышении начинается разрушение материала. В реальности разрушение начинается при меньших значениях, поскольку строение реальных образцов неоднородно. Это вызывает неравномерное распределение напряжений, и разрушение начинается с тех участков, где напряжения максимальны.